SLU
EAS-A193 Class Notes
|
SLU EAS-A193 Class Notes |
|
The magnitude is the most often cited measure of an earthquake's size, but it is not the only measure, and in fact, there are different types of earthquake magnitude. Early estimates of earthquake size were based on non-instrumental measures of the earthquakes effects. For example, we could use values such as the number of fatalities or injuries, the maximum value of shaking intensity, or the area of intense shaking. The problem with these measures is that they don't correlate well. The damage and devastation produced by an earthquake will depend on its location, depth, proximity to populated regions, as well as its "true" size. Even for earthquakes close enough to population centers values such as maximum intensity and the area experiencing a particular level of shaking did not correlate well.
With the invention and deployment of seismometers it became possible to accurately locate earthquakes and measure the ground motion produced by seismic waves.
 |
|
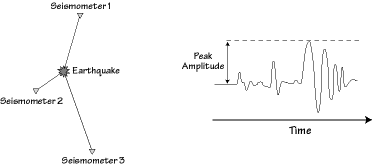
The development and deployment of seismometers lead to many changes in earthquake studies, magnitude was the first quantitative measure of earthquake size based on seismograms. The maximum or "peak" ground motion is defined as the largest absolute value of ground motion recorded on a seismogram. In the example above the surface wave has the largest deflection, so it determines the peak amplitude. |
It was natural for these instrumental measures to be used to compare earthquakes, and one of the first ways of quantifying earthquakes using seismograms was the magnitude.
In 1931 a Japanese seismologist named Kiyoo Wadati constructed a chart of maximum ground motion versus distance for a number of earthquakes and noted that the plots for different earthquakes formed parallel, curved lines (the larger earthquakes produced larger amplitudes). The fact that earthquakes of different size generated curves that were roughly parallel suggested that a single number could quantify the relative size of different earthquakes.
In 1935 Charles Richter constructed a similar diagram of peak ground motion versus distance and used it to create the first earthquake magnitude scale (a logarithmic relationship between earthquake size and observed peak ground motion). He based his scale on an analogy with the stellar brightness scale commonly used in astronomy which is also similar to the pH scale used to measure acidity (pH is a logarithmic measure of the Hydrogen ion concentration in a solution).
 |
|
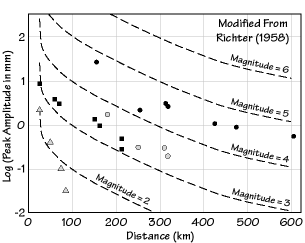
Sample of the data used by Richter to construct the magnitude scale for southern California. The symbols represent observed peak ground motions for earthquakes recorded during January of 1932 (different symbols represent different earthquakes). The dashed lines represent the reference curve for the decrease in peak-motion amplitude with increasing distance from the earthquake. A magnitude 3.0 earthquake is defined as the size event that generates a maximum ground motion of 1 millimeter (mm) at 100 km distance. |
To complete the construction of the magnitude scale, Richter had to establish a reference value and identify the rate at which the peak amplitudes decrease with distance from an earthquake. He established a reference value for earthquake magnitude when he defined the magnitude as the base-ten logarithm of the maximum ground motion (in micrometers) recorded on a Wood-Anderson short-period seismometer one hundred kilometers from the earthquake. Richter was pragmatic in his definition, and chose a value for a magnitude zero that insured that most of the earthquakes routinely recorded would have positive magnitudes. Also, the Wood-Anderson short-period instrument that Richter chose for his reference records seismic waves with a period of about 0.8 seconds, roughly the vibration periods that we feel and that damage our buildings and other structures.
 |
|
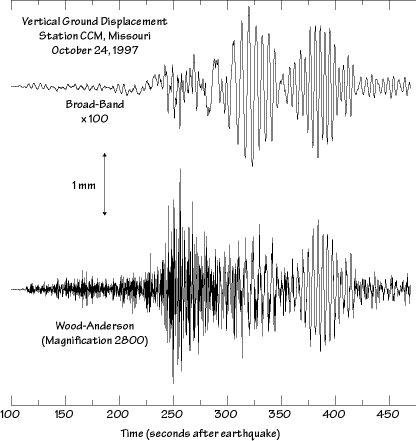
Example seismogram recorded on a Wood-Anderson short period seismogram. The top waveform shows the broad-band displacement, the lower trace shows the corresponding ground motion that would register on a Wood-Anderson seismograph. |
Richter also developed a distance correction to account for the variation in maximum ground motion with distance from an earthquake (the dashed curves shown in the above diagram show his relationship for southern California). The precise rate that the peak ground motions decrease with distance depends on the regional geology and thus the magnitude scale for different regions is slightly dependent on the "distance correction curve".
Thus originally, Richter's scale was specifically designed for application in southern California. Richter's method became widely used because it was simple, required only the location of the earthquake (to get the distance) and a quick measure of the peak ground motion, was more reliable than older measures such as intensity. It became widely used, well established, and forms the basis for many of the measures that we continue to use today. Generally the magnitude is computed from seismographs from as many seismic recording stations as are available and the average value is used as our estimate of an earthquake's size.
We call the Richter's original magnitude scale ML (for "local magnitude"), but the press usually reports all magnitudes as Richter magnitudes.
To study earthquakes outside southern California, Richter extended the concepts of his local magnitude scale for global application. In the 1930's through the 1950's together with Beno Gutenberg, Richter constructed magnitude scales to compare the size of earthquakes outside of California. Ideally they wanted a magnitude scale that gave the same value if the earthquake is recorded locally or from a great distance. That way you could compare the seismicity of earthquakes in different parts of Earth. But the extension of methods to estimate the local magnitude is complicated because the type of wave generating the largest vibrations and the period of the largest vibrations recorded at different distances from an earthquake varies. Near the earthquake the largest wave is a short-period S-wave, at greater distances longer-period surface waves become dominant.
To exploit the best recorded signal (the largest) magnitude scales were developed for "teleseismic" (distant) observations using P waves or Rayleigh waves. Eventually the teleseismic P-wave scale became known as "body-wave magnitude" and the Rayleigh wave based measure came to be called "surface-wave magnitude". The surface-wave magnitude is usually measured from 20s period Rayleigh waves, which are very well transmitted along Earth's surface and thus usually well observed.
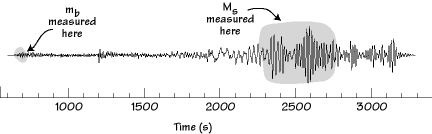 |
|
Gutenberg and Richter developed two magnitudes for application to distant earthquakes: mb is measured using the first five seconds of a teleseismic (distant) P-wave and Ms is derived from the maximum amplitude Rayleigh wave. |
There are several problems associated with using magnitude to quantify earthquakes, and all are a direct consequence of trying to summarize a process as complex as an earthquake in a single number. First, since the distance corrections depend on geology each region must have a slightly different definition of local magnitude. Also, since at different distances we rely on different waves to measure the magnitude, the estimates of earthquake size don't always precisely agree. Also, deep earthquakes do not generate surface waves as well as shallow earthquakes and magnitude estimates based on surface waves are biased low for deep earthquakes.
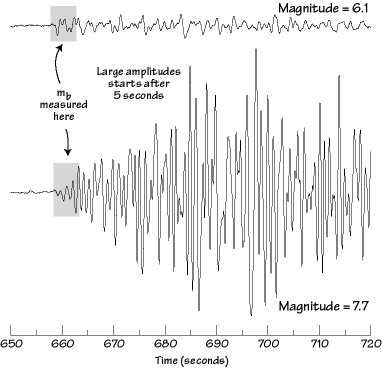
Also, measures of earthquake size based on the maximum ground shaking do not account for another important characteristic of large earthquakes - they shake the ground longer. Consider the example shown in the diagram below. The two seismograms are the P-waves generated by magnitude 6.1 and 7.7 earthquakes from Kamchatka. The body-wave magnitude for these two earthquakes is much closer because the rule for estimating body-wave magnitude is to use the maximum amplitude in the first five seconds of shaking. As you can see, the difference in early shaking between the two earthquakes is much less than the shaking a little bit later which indicates the larger difference in size.
 |
|
Teleseismic (distant) P-waves generated by two earthquakes in Kamchatka and recorded at station CCM, Cathedral Caves, MO, US. The signals that would be recorded on a on a short-period seismometer are shown using the same scale. The time is referenced to the onset of rupture for each earthquake. |
Even after 5 seconds the amplitude ratio of these P waves does not accurately represent the difference in size of these two earthquakes. The magnitude 6.1 event probably ruptured for only a few seconds, the magnitude 7.7 ruptured for closer to a minute.
Another measure of earthquake size is the area of the fault that slipped during the earthquake. During large earthquakes the part of the fault that ruptures may be hundreds of kilometers long and 10s of kilometers deep. Smaller earthquake rupture smaller portions of the fault. Thus the area of the rupture is an indicator of the earthquake size.
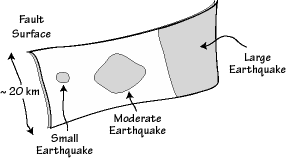 |
|
The size of the area that slips during an earthquake is increases with earthquake size. The shaded regions on the fault surface are the areas that rupture during different size events. The largest earthquakes generally rupture the entire depth of the fault, which is controlled by temperature. The temperature increases with depth to a point where the rocks become plastic and no longer store the elastic strain energy necessary to fail suddenly. |
Usually we estimate fault rupture areas using the location of aftershocks, but we may also estimate the area of rupture from seismograms if the observations are of high quality.
Another measure of an earthquake size is the dimension of the offset produced during an earthquake - that is, how far did the two sides move? Small earthquakes have slips that are less than a centimeter, large earthquakes move the rocks about 10-20 meters.
Seismic moment is a quantity that combines the area of the rupture and the amount of fault offset with a measure of the strength of the rocks - the shear modulus m.
Usually we measure the moment directly from seismograms, since the size of the very long-period waves generated by an earthquake is proportional to the seismic moment. The physical units of seismic moment are force x distance, or dyne-cm.
For scientific studies, the moment is the measure we use since it has fewer limitations than the magnitudes, which often reach a maximum value (we call that magnitude saturation).
To compare seismic moment with magnitude, Mw , we use a formula constructed by Hiroo Kanamori of the California Institute of Seismology:
where the units of the moment are in dyne-cm.
The symbols used to represent the different magnitudes are
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*at the distances appropriate for local magnitude, either the S-wave or the surface waves generally produce the largest vibrations.
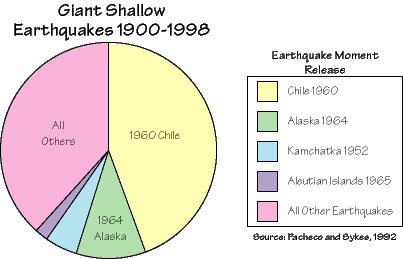
The seismic moment and moment magnitude give us the tool we need to compare the size of the largest quakes. We find that the "moment release" in shallow earthquakes throughout the entire century is dominated by several large subduction zone earthquake sequences. First, let's compare the amount of energy released in the different plate settings:
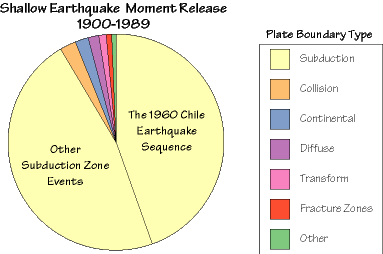
or we can just compare the largest four earthquakes (those with magnitudes greater than 9) with all the other shallow earthquakes.