Inversion Programs
The output of the inversion programs consists of two components. A text file that contains several items describing the input SAC files and Green's functions, as well as the moment-tensor estimate and misfit values from the inversion. Also computed are predicted SAC waveforms which for mtinv have names that have the prefix "p_" and the rest of the name is the same as the input file name. The prefix for l1mtinv is "l1p_", for the grid search program the prefix is "gs2_" (grid-search L2 norm).
Grid Search
The output file for the grid search contains the misfit for all values of strike, dip, and rake investigated. The file format is quite simple:
strike dip rake fractional_misfit(L2) total_misfit(L2) fractional_misfit(L1) total_misfit(L1)
The values can be converted to other formats using awk and contoured or plotted using SAC. For example, to see the misfit as a function of strike
> awk '{print $1, $3}' >! Misfit_vs_Strike
> sac
sac> ra content p Misfit_vs_Strike
sac> line off; symbol on
sac> p
sac> quit
>
You could write a simple program to do something more sophisticated to the file like stripping out only the minimum error for each strike and decreasing the size of the file and the number of points plotted.
An example (mtinv)
Below are examples from a homework problem in one of my seismology courses. The students are required to request and prepare data from the IRIS data management center for an inversion of seven P-waveforms generated by the 1994 Northridge, California earthquake (I use seven to keep the IRIS data request small and to keep the number of files that the students have to study small).
Here's a listing of the files in an inversion directory (I create a separate directory for each depth). The *_dsp.z are the observations, the *_pz.??? are the Green's functions, and the p_*_dsp.z are the predictions. Other files are associated with computing the teleseismic responses (I used Chuck Langston's generalized ray codes to do that). I convolved a 12-second wide triangle with the Green's functions for this inversion.
ALE_dsp.z bdfb_pz.iso fa.in hrv_pz.vds p_MAJO_dsp.z BDFB_dsp.z bdfb_pz.vds fa.in.p hrv_pz.vss p_SJG_dsp.z COL_dsp.z bdfb_pz.vss farray.out infile p_gftns* ESK_dsp.z cleanup* ffs.in majo_pz.clv p_response* HRV_dsp.z col_pz.clv ffs.in.d majo_pz.iso sjg_pz.clv MAJO_dsp.z col_pz.iso ffs.in.p majo_pz.vds sjg_pz.iso README col_pz.vds ffsynth.out majo_pz.vss sjg_pz.vds SJG_dsp.z col_pz.vss fit.ps outfile sjg_pz.vss ale_pz.clv doall.csh fit.sgf p_ALE_dsp.z trapezoid ale_pz.iso esk_pz.clv fort.7 p_BDFB_dsp.z ale_pz.vds esk_pz.iso fort.8 p_COL_dsp.z ale_pz.vss esk_pz.vds hrv_pz.clv p_ESK_dsp.z bdfb_pz.clv esk_pz.vss hrv_pz.iso p_HRV_dsp.z
Here's the output file (the depth of the synthetic seismograms was 10 km, but I forgot to include that information in the Green's function header, so the mtinv complained and used a value of -12345.0 for the depth (the "undefined" value for SAC).
*********** L2 INVERSION **********************
Moment Tensor Inversion using mtinv:
Inversion run on: Mon Apr 6 13:59:47 1998
Information from header of first data file:
Reference Time: JAN 17 (017), 1994 12:39:04.098
Origin time (s) relative to reference: 0.
Event Lat,Lon: 34.210 -118.540
Greens Function summary:
basename = ale_pz
npts = 63 dt = 1.00000 depth = -12345.0
Data summary:
basename = ALE_dsp.z
npts = 63 dt2 = 1.00000
Sum of Square Amplitudes: 2171.42
Weight: 1.00000
Greens Function summary:
basename = bdfb_pz
npts = 63 dt = 1.00000 depth = -12345.0
Data summary:
basename = BDFB_dsp.z
npts = 63 dt2 = 1.00000
Sum of Square Amplitudes: 1224.15
Weight: 1.00000
Greens Function summary:
basename = col_pz
npts = 63 dt = 1.00000 depth = -12345.0
Data summary:
basename = COL_dsp.z
npts = 63 dt2 = 1.00000
Sum of Square Amplitudes: 1614.10
Weight: 1.00000
Greens Function summary:
basename = esk_pz
npts = 63 dt = 1.00000 depth = -12345.0
Data summary:
basename = ESK_dsp.z
npts = 63 dt2 = 1.00000
Sum of Square Amplitudes: 1179.04
Weight: 1.00000
Greens Function summary:
basename = hrv_pz
npts = 63 dt = 1.00000 depth = -12345.0
Data summary:
basename = HRV_dsp.z
npts = 63 dt2 = 1.00000
Sum of Square Amplitudes: 1953.42
Weight: 1.00000
Greens Function summary:
basename = majo_pz
npts = 63 dt = 1.00000 depth = -12345.0
Data summary:
basename = MAJO_dsp.z
npts = 63 dt2 = 1.00000
Sum of Square Amplitudes: 1426.54
Weight: 1.00000
Greens Function summary:
basename = sjg_pz
npts = 63 dt = 1.00000 depth = -12345.0
Data summary:
basename = SJG_dsp.z
npts = 63 dt2 = 1.00000
Sum of Square Amplitudes: 2127.77
Weight: 1.00000
Using a total of 441 points in inversion.
Singular Values of A**t A:
1.95335E-08
5.47743E-09
2.08584E-09
3.57088E-10
1.02269E-09
Singular Values of A:
1.39762E-04
7.40097E-05
4.56711E-05
1.88968E-05
3.19796E-05
--------- From Subroutine Moment ---------------
Input moment tensor:
0.853E+06 0.172E+06 0.480E+06
0.172E+06 0.330E+06 -0.459E+05
0.480E+06 -0.459E+05 -0.118E+07
m0 = 1.00000E+20
Isotropic Component: 0.
Subtracted out the isotropic component.
The Deviatoric Moment Tensor:
0.853E+06 0.172E+06 0.480E+06
0.172E+06 0.330E+06 -0.459E+05
0.480E+06 -0.459E+05 -0.118E+07
eigenvalues of the moment tensor
0.998E+06 0.296E+06 -0.129E+07
and associated eigenvectors (in the columns)
-0.951E+00 0.214E+00 -0.222E+00
-0.231E+00 -0.972E+00 0.510E-01
-0.204E+00 0.996E-01 0.974E+00
Eigenvector 1:
Az = 13.6313 Plunge = 11.7974
Eigenvector 2:
Az = 282.433 Plunge = 5.71809
Eigenvector 3:
Az = 167.046 Plunge = 76.8538
The Total Scalar Moment (Silver&Jordan,1982) is
0.117E+27
The Total Moment Magnitude (Kanamori(1979)) is
6.7
The Deviatoric Scalar Moment (Silver&Jordan,1982) is
0.117E+27
The Deviatoric Moment Magnitude (Kanamori(1979)) is
6.7
double couple eigenvalues= 0.115E+07 -0.115E+07
error (clvd/dc)*100= 45.782
moment tensor for the major dislocation
0.8559 0.0506 0.2308 0.4103 -0.0025
pole vectors p1 and p2
0.516E+00 0.199E+00 0.833E+00
-0.829E+00 -0.127E+00 0.544E+00
azimuth and plunge of pole #1; az1= 21.11 pl1= 56.42
azimuth and plunge of pole #2; az2= 188.71 pl2= 32.96
fault angle parameters
strike dip rake
111.11 33.58 100.38
278.71 57.04 83.18
--------------------------------------------------
Covariance Matrix
xx yy xy xz yz
0.117E+10
-0.105E+10 0.120E+10
0.598E+09 -0.596E+09 0.154E+10
0.119E+09 0.781E+08 0.116E+08 0.328E+09
0.326E+08 0.104E+09 0.327E+08 0.996E+08 0.256E+09
file,weight,sum_square_error,fractional_error,ls_scale_factor
ALE_dsp.z 0.100000000E+01 0.949896362E+03 0.437454700E+00 0.106386065E+01
BDFB_dsp. 0.100000000E+01 0.126978683E+03 0.103727728E+00 0.947091341E+00
COL_dsp.z 0.100000000E+01 0.485019897E+03 0.300489992E+00 0.960329473E+00
ESK_dsp.z 0.100000000E+01 0.487186737E+03 0.413205385E+00 0.102568638E+01
HRV_dsp.z 0.100000000E+01 0.402081848E+03 0.205835089E+00 0.994883895E+00
MAJO_dsp. 0.100000000E+01 0.526168091E+03 0.368842036E+00 0.131090260E+01
SJG_dsp.z 0.100000000E+01 0.351402039E+03 0.165150419E+00 0.933144391E+00
Misfit Summary:
Fractional Misfit: 0 1
| | | | |
ALE_dsp.z 0.44 |xxxxxxxxxxxxxxxxxxxxx |
BDFB_dsp.z 0.10 |xxxxx |
COL_dsp.z 0.30 |xxxxxxxxxxxxxxx |
ESK_dsp.z 0.41 |xxxxxxxxxxxxxxxxxxxx |
HRV_dsp.z 0.21 |xxxxxxxxxx |
MAJO_dsp.z 0.37 |xxxxxxxxxxxxxxxxxx |
SJG_dsp.z 0.17 |xxxxxxxx |
| | | | | |
Unweighted SSE,Weighted SSE,Unweighted RMS,Weighted RMS
7.65226 7.65226 2.76627 2.76627
Total Error divided by sum of all seismogram amplitudes
Unweighted, weighted
0.284594 0.284594
Covariance Matrix
xx yy xy xz yz
0.894E+10
-0.803E+10 0.918E+10
0.458E+10 -0.456E+10 0.118E+11
0.914E+09 0.598E+09 0.891E+08 0.251E+10
0.250E+09 0.795E+09 0.250E+09 0.762E+09 0.196E+10
A macro to compare observed and predicted waveforms
All the misfit information is summarized in the output file but nothing beats a careful inspection of the waveforms and you should compare the observed and predicted waveforms using SAC. To ease the comparison, you choose a consistent suffix for your input files (such as _dsp.z, _dsp.r, _dsp.t). Here's a sample macro to compare the *_dsp.z files:
|
The Macro |
Comments |
* plot obs and predicted seis * qdp off color on inc on list r b xlabel "time @(s@)" fileid off * setbb x0 0.05 setbb y0 0.75 setbb w 0.2 setbb h 0.15 setbb gh 0.15 setbb gw 0.1 * setbb left %x0 evaluate to right %left + %w setbb bot %y0 evaluate to top %bot + %h * begfr * * do pred wild p_*dsp.z * setbb obs ( AFTER "p_" $pred ) * xvp %left %right yvp %bot %top * r $pred %obs ch nzmin udef; ch b 0; ch a undef; title ' (CONCAT ' &2,kstnm ' ) p2 * evaluate to left %right + %gw evaluate to right %left + %w * if %right gt 1.0 setbb left %x0 evaluate to right %left + %w evaluate to bot %bot - %gh - %h evaluate to top %bot + %h * if %bot lt 0.0 endfr evaluate to bot %y0 evaluate to top %bot + %h begfr endif * endif * enddo endfr |
Set up some graphics parameters
These parameters will be used to scale and
|
Here's the result of the macro for the example shown above:
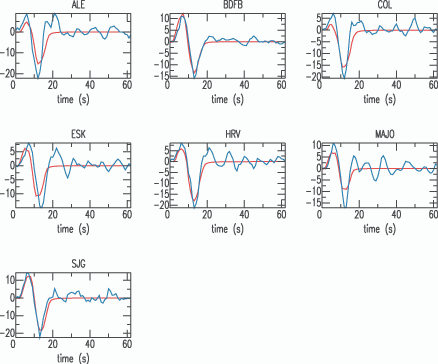
The observed are shown as blue lines, the predicted as red. The predictions are computed using a layer-over a half-space for this simple homework exercise.
Most of the macro is some bookkeeping to check for when a column or page has filled up. You could add another loop to display radial and transverse components - keying on the vertical.